最优控制与强化学习：定义，概念解析和技术学习路线

前言

2012 年 12 月，NASA 和 spaceX 的三个工程师发表了一篇论文名为《Lossless Convexification of Non-Convex Control Bound and Pointing Constraints of the Soft Landing Optimal Control Problem》（对软着陆最优控制问题中存在的非凸控制约束和朝向约束进行无损凸化），就是这篇文章让可回收火箭成为可能，可能是过去 10 年航空航天领域最有影响力的一份工作。2016 年 3 月，计算机程序 AlphaGo (Silver et al., 2016) 在超大搜索空间和局面评估难度较高的围棋问题上以 4：1 的成绩击败了曾获 18 次世界冠军的围棋手李世石。2019 年 4 月，OpenAI Five 在部分可观测状态(partial observation states)的 5V5 高难度 dota2 游戏中，以 2:0 击败了 Dota2 TI8 冠军 OG 战队。2020 年国际上围绕德州扑克这一大规模不完美信息博弈问题的优化求解取得了长足进步，加拿大阿尔伯特和美国卡内基梅隆大学的研究者设计的 AI 程序在两人和 6 人无限注德州扑克中战胜了人类专业选手。

这些研究问题可以抽象为同一类研究问题：序列决策问题（sequencial decision-making problem），也就是要找到最优的一个序列动作，使得特定问题下的目标函数最大化。背后用到的技术算法共同指向了一个一体两面的研究领域：最优控制 (optimal control) 和深度强化学习 (deep reinforcement learning) 。这引起了我的极大兴趣，也是我当时能够看到的通往通用人工智能为数不多的路线，我暗暗下定决心要精通这一领域，作为最长期的技术投资。

如果去寻找资料会发现，最优控制这门课程主要分布在电气工程学科（Electrical Engineering; 自动化控制，信号处理，机器人动力学与控制等），机械工程学科(Mechanical Engineering; 动力系统，机械系统控制，机器人学等)和航空航天学科（Aerospace；导航系统，飞行器控制等），深度强化学习这门课程主要聚集在计算机科学学科（Computer Science；深度学习，计算机视觉，强化学习），考虑到计算机科学近 10 年极强的开源精神，以及我的一些背景，我首先以深度强化学习作为开端开始了我的探索之旅。学习了 Sutton 的《Reinforcement Learning: An Introduction》，Deepind Silver 以及 OpenAI 的《deep reinforcement learning》以及 stanford 和 bekerley 的深度强化学习公开课，对深度强化学习的问题设定，概念框架，理论推倒和代码实现有了深入理解，但同时也发现了一些困难，困难主要有两点，一是论文中对一个相似问题的解决思路和研究方法纷繁杂乱，让我产生了对这个大领域不够系统缺少全貌的零散感，比如核心都是基于动态规划算法，最优控制中常常出现的概念是 differential dynamic programming 而强化学习中常出现的是 approximate dynamic programming；二是对这一领域研究范式有突破性的论文，看似能理解她的原理和代码，但缺失的是不清楚作者如何从根源上想到的这个研究 idea 以及如何在一个重要论文的基础上做一些稍微具有显著意义的改进。这不是我想要的状态，痛定思痛，我决定追根溯源，去探索清楚这个领域背后更清晰的全貌。

我把个人的理解和思考写在这里，在这篇文章中，我想要通过 high-level 的视角，探究最优控制与深度强化学习背后统一的全貌是什么以及这两个领域的核心联系以及区别点，试图填补最优控制与强化学习之间的在认知层面的 gap. 目录如下：

Part I: 研究问题的设定
Part II: 最优控制与强化学习的核心联系与区别
Part III: 最优控制与强化学习的技术学习路线

Part I: 研究问题的设定

序列决策问题可以统一抽象为如下的一个优化问题： deterministic_optimal_control_discret_time

这里的核心理解主要有两点：

1 如何理解一个系统的动态方程

x_{t+1} = f(x_t, a_t)

1.a 一个系统 (任何一个系统，飞行器/机器人/交易系统等) 在 t 时刻的状态可以被一个 n 维的向量所表示，记为 $x_t$ , 对这个系统在 t 时刻做的各种操作可以被一个 m 维的向量表示，记为 $a_t$ 。

1.b 对这个系统在 r 时刻做一个动作操作 $a_t$ , 会改变系统的状态，其 t+1 时刻所处的状态用 $x_{t+1}$ 表示，也就是说一个系统在 t+1 时刻所处的状态是 t 时刻的状态 $x_t$ 和 t 时刻动作 $a_t$ 的一个函数。不同研究问题，x，a 以及 f 的具体表达式存在差异。

2 这个优化问题的含义是什么，我们最终要解决什么问题？

给定一个满足状态方程约束和其他约束的状态序列 $x_{1:N}$ 和动作序列 $a_{1:N−1}$ ,根据目标函数，就会得到一个数值，我们的目标是，在满足约束的条件下，找到那个使目标函数值最小所对应的序列 $(x_1,a_1,x_2,a_2,...,x_{n−1},a_{n−1},x_n)$ 。

不同专业来源的论文在研究问题的设定上会让读者存在一些困扰，困扰的来源主要来源于两点：

1 连续时间最优控制和离散时间最优控制的区别

上面的内容给出的是最优控制问题的离散时间版本，下面我给出最优控制的连续时间版本：

与离散时间版本的问题设定相比，差异点除了离散版本的求和符号 ∑ 与积分符号 ∫ 的差异外，差异的重点在动态函数的表达上。连续时间的动态函数往往以一个叫做普通微分方式 (Ordinary Differential Equation, ODE) 的东西来表达当前状态，当前动作与状态变化之间的关系，在这里我们只需要知道，存在一些数值计算的方法（比如欧拉方法，Runge-Kutta methods 等）可以将一个普通微分方程转换为离散函数的表达，即可以将 $\dot{x}(t) = f(x(t),a(t),t)$ 转化为 $x_{t+1} = f(x_t, a_t)$ ，我们只是缺失了本该在上学时就学习但从未被提及以及重视的数值计算技巧而已。

2 确定性最优控制和随机最优控制的区别

在此之前，我们讨论的最优控制问题，都是假定 dynamic function 是一个确定性的函数，即系统在 t+1 时刻所处的状态 $x_{t+1}$ 是 t 时刻的状态 $x_t$ 和 t 时刻动作 $a_t$ 的一个函数,也就是说给定 $x_t$ , $a_t$ ,在函数 f 的作用下会得到唯一确定的向量 $x_{t+1}$ ，我们把这样设定的最优控制问题定义为确定性的最优控制问题（deterministic optimal control problem）。确定性最优控制问题涵盖了工科研究内容 90%的场景，因为在物理层面，大部分场景都是确定的作用过程，这些系统的 dynamic function 可以精确建模，例如机械系统控制，电机控制，假定无干扰的机器人系统等。但是一些研究领域所面临的系统存在一些不确定性，这个不确定性有两个来源，一是一个确定性的系统会受到随机噪声扰动的影响，让其变得具有一定的不确定性，例如传感器噪声下的机器人研究，受气动不确定影响的飞行器控制研究。二是系统自身就是一个随机系统，如基于金融价格变化的交易系统。带有一定不确定的系统可以用随机动态函数进行建模，离散版本的情况是 $x_{t+1}=f(x_t,a_t,t)+w_t$ , 其中 $w_t$ 是一个假定已知概率分布的随机变量（如高斯分布）。在这个设定下， $x_t$ 也变为了一个 n 维向量的随机变量。由于 $x_t$ 是一个随机变量，我们的目标函数，变为对 N 个阶段损失值进行求期望 E 操作，如果一个最优控制问题的动态系统具有一定的随机性，我们将该研究问题定义为随机最优控制问题（stochastic optimal control problem），设定如下：

在连续时间的随机最优控制场景中，随机系统的动态函数，被一个称作为随机微分方程（Stochstic Differential Equation, SDE）的东西所表示，不要被其暂时丑陋的外表震慑退，在这里，唯一需要知道的就是，存在一些数值计算的方法（如 Euler-Maruyama，Milstein 等）可以将一个随机微分方程

dx(t) =f(x(t),a(t),t) + \sigma (x(t),a(t),t)dW(t)

离散化的表示为

x_{t+1} = f(x_t, a_t,t) + w_t

stochastic_optimal_control_continous_time

至此，对最优控制以及强化学习的问题设定有了全貌的认识。

Part II: 最优控制与强化学习的核心联系与区别

为什么说最优控制与强化学习是一个一体两面的研究领域，因为他们问题设定的内核完全一致，区别点体现在以下几个方面：

在最优控制中语境中，目标函数中的 L 常常表示为 Stage Cost Funtion，用来度量给定 x 和 a 之后承担的损失是多少，因此最优控制的目标是一个求解最小化的优化问题，即我要一个序列 $(x_1,a_1,x_2,a_2,...,x_{n−1},a_{n−1},x_n)$ 在满足约束的基础上，使得目标函数值最小。在强化学习的语境中，目标函数中的 L 常常表示为 Stage Reward Function，用来表示给定 x 和 a 之后得到的奖励是多少，因此最优控制的目标是一个求解最大化的优化问题，即我要一个序列 $(x_1,a_1,x_2,a_2,...,x_{n−1},a_{n−1},x_n)$ 在满足约束的基础上，使得目标函数值最大。
第二个差异体现体现在研究侧重点，最优控制目前更多的研究问题侧重在确定性的最优控制，而强化学习原生的侧重点就是随机最优控制。导致这个侧重点产生的原因主要是工科（电气工程，机械工程，航空航天）语境下的系统的动态函数大都是确定性的，所以前期积累的研究工作大都集中在确定性的最优控制，而强化学习原生的就在解决 MDP（markov decision process）的随机动态系统，所以更关注随机最优控制。但是随着学术研究越来越重视系统的扰动因素，比如考虑气动因素对飞行器控制的影响，以及从仿真环境迁移到现实环境过程中对机器人控制产生的扰动性，越来越多的研究开始重视随机最优控制的研究。
以上的两点仅仅是研究问题设定层面的相对较小的异同，从我个人的理解看，最优控制与强化学习真正的核心区别点在于：在最优控制语境下，系统的动态函数（dynamic function）以及损失函数(stage cost function)是具有显示表达式的函数（explictic function），可以直接求函数的梯度。但在强化学习的语境下，系统的动态函数（dynamic function）以及损失函数（stage cost function）仅仅是两个隐式的函数，只能填入输入得到输出值，无法得到其函数显示的表达式，因此更无法求函数的梯度。这一核心差异直接决定了求解最优控制问题以及强化学习问题的技术路线的差异。在最优控制的语境下，求解最优控制问题主要有两条路线，一是直接优化法。因为有函数表达式，所以可以将序列 $(x_1,a_1,x_2,a_2,...,x_{n−1},a_{n−1},x_n)$ 直接作为决策变量，将动态函数转换为约束连同其他约束，放入优化器中，直接使目标函数最小化所对应的那个最优序列，这类方法可以统一称为直接配点法（direct collocation）。二是动态规划法（dynamic programming），动态规划法的核心思路是基于最优化原则得到贝尔曼方程，然后因为知道动态函数的函数表达式，因此可以使用泰勒级数扩展的方法（需要用到函数的一阶导二阶导信息）对未来的价值函数进行近似估计，这一类方法统一称为微分动态规划（Differential Dynamic Programming,DDP）。在强化学习的语境下，由于无法得知动态函数以及成本函数的显示表达式，因此无法进行 direct collocation 以及 DDP,但强化学习找到了属于他自己的两条安身立命的路线。一是策略优化法，通过参数化的方式（比如一个神经网络）构建从状态到动作的一个映射关系 at=uθ(xt) 该函数称之为策略，原来的优化问题，转变化找到一个最优的参数 θ ，使得目标函数最大化。二是动态规划法，是的，强化学习的问题求解根基也依然是动态规划算法，动态规划算法的起点依然是基于最优化原则得到贝尔曼方程，与最优控制语境不同的是，因为无法得到函数的显示表达式，因此无法通过泰勒扩展的方法得到价值函数的近似估计，因此强化学习的思路是，通过参数化的方式(比如一个神经网络)构建从状态到价值的一个映射关系 $v_t=g_θ(x_t)$ ，通过样本迭代优化的思路优化价值网络，从而可以得到最优状态动作序列 $(x_1,a_1,x_2,a_2,...,x_{n−1},a_{n−1},x_n)$ 。

Part III: 最优控制与强化学习的技术学习路线

成长速度最快的方式是模仿，在机器人领域，同时关注最优控制和强化学习这两个方向、相对活跃、有重要影响力产出且重视开源的学者和及其实验室，我关注的是这几个：

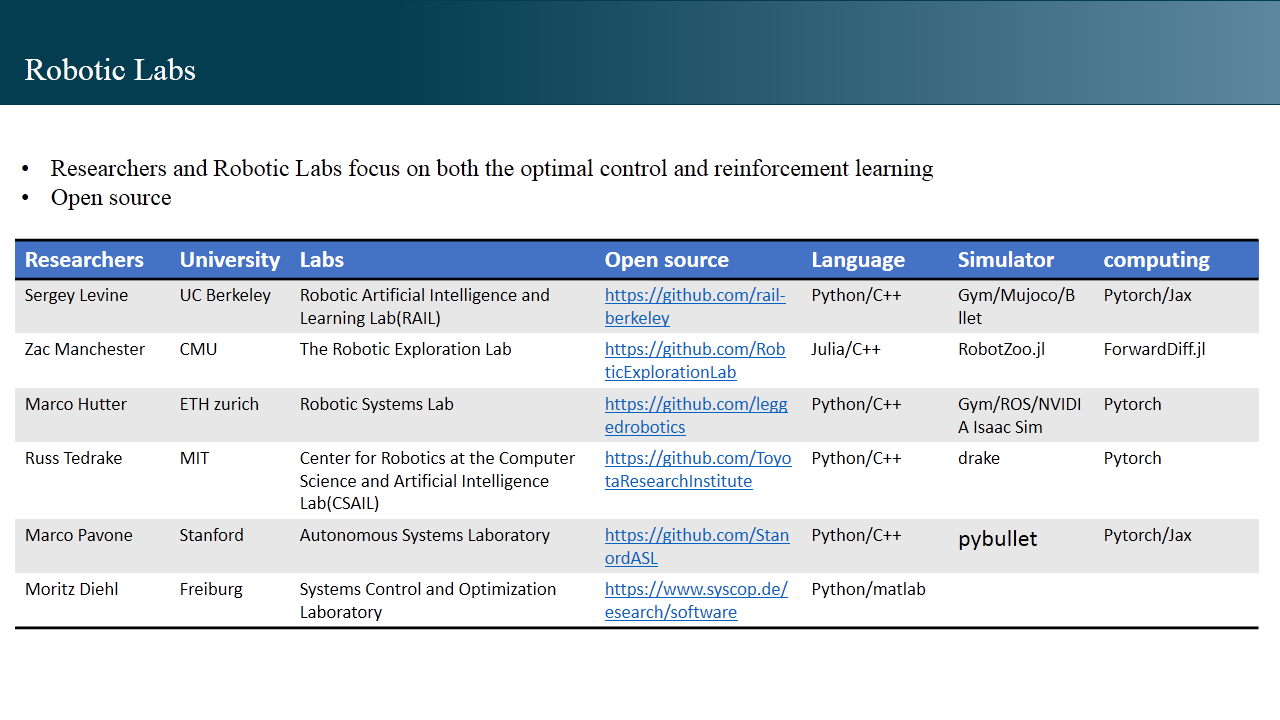
Zac Manchester 侧重的是最优控制，Sergey Levine 侧重的是强化学习，Marco Hutter 完成了从最优控制到强化学习的过渡，现在主要关注基于深度强化学习进行机器人的控制。编程语言方面主流的开源环境和代码所需要的编程语言，上层是 Python，Julia，底层依然是 C++。

如果想要把这个领域的基本功打扎实，我觉得最优的行进路线可以是数值计算-数值优化-最优控制-深度学习-最优控制与强化学习-深度强化学习，每一部分走主线剧情，整个知识体系会相对平滑很多。 roadmap

后记

最优控制和强化学习是一门高度交叉的学科，结合了数学，计算机科学和多个工程领域的复合知识。她要求先基于领域知识对一个系统（环境）进行建模，然后基于最优控制的设定，使用不同的算法进行数值求解。

从数学角度看，她涉及到不同程度的微积分，概率论，随机过程，深度学习，最优化理论；从编程角度看，她不仅需要那些能够将数学相关理论落地到计算机程序中的数值计算，数值优化技巧，还需要掌握高性能计算，以应对现实应用中的实时性要求。然而这些技术挑战的背后也让我们看到了去控制复杂机器人的可能性，从机械臂，四足机器人，自动驾驶，人形机器人到无人机，超高音速飞行器，可回收火箭，太空飞船，那些原本仅仅存留在科幻电影，科幻小说中的浪漫幻想，也开始一点一点照进现实。

文章的最后，我想以美国前总统约翰·费茨杰拉德·肯尼迪（John Fitzgerald Kennedy）于 1962 年 9 月 12 日在赖斯大学的一篇关于航天探索演讲的一段话作为结束。这篇演讲，《We Choose to Go to the Moon》，被视为阿波罗登月计划奠基的第一铲土。肯尼迪本人于 1963 年遇刺身亡，登月计划由约翰逊总统与尼克松总统接管。经过不懈努力，终于在 1969 年 7 月成功将人类送上了月球。

But why, some say, the moon?

Why choose this as our goal?

And they may well ask why climb the highest mountain?

Why, 35 years ago, fly the Atlantic?

Why does Rice play Texas?

We choose to go to the moon.

We choose to go to the moon in this decade and do the other things

Not because they are easy, but because they are hard

Because that goal will serve to organize and measure the best of our energies and skills

Because that challenge is one that we are willing to accept

One we are unwilling to postpone, and one which we intend to win and the others, too.

但是，有人问，为什么选择登月？

为什么选择登月作为我们的目标？

那他们完全可以问

为什么要登上最高峰

为什么 35 年前要飞越大西洋？

为什么赖斯大学要和德克萨斯大学进行（橄榄球）比赛？

我们决定登月

我们决定在这十年间登月，并且完成其他事

不是因为它们轻而易举而是因为它们困难重重

因为这个目标将有助于统筹和衡量我们最佳的能源和技术

因为这个挑战是我们乐于接受的

是我们不愿推迟的

是我们志在必得的

其他的挑战亦是如此